Analiza tensiunii, ramura matematicii în legătură cu relațiile sau legile care rămân valabile indiferent de sistemul de coordonate utilizat pentru a specifica cantitățile. Astfel de relații sunt numite covariante. Tensorii au fost inventați ca o extensie a vectorilor pentru a formaliza manipularea entităților geometrice care apar în studiul multiplelor matematice.
Un vector este o entitate care are atât amploarea cât și direcția; este reprezentabilă printr-un desen al unei săgeți și se combină cu entități similare în conformitate cu legea paralelogramului. Din cauza acestei legi, un vector are componente - un set diferit pentru fiecare sistem de coordonate. Când sistemul de coordonate este schimbat, componentele vectorului se schimbă conform unei legi matematice de transformare deductibile din legea paralelogramului. Această lege a transformării componentelor are două proprietăți importante. În primul rând, după o secvență de modificări care se termină în sistemul de coordonate inițial, componentele vectorului vor fi aceleași ca la început. În al doilea rând, relațiile dintre vectori - de exemplu, trei vectori U, V, W, astfel încât 2U + 5V = 4W - vor fi prezenți în componente, indiferent de sistemul de coordonate.
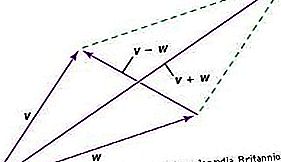
Prin urmare, un vector poate fi considerat ca o entitate care, în spațiul n-dimensional, are n componente care se transformă în conformitate cu o lege specifică a transformării având proprietățile de mai sus. Vectorul în sine este o entitate obiectivă independentă de coordonate, dar este tratată în termeni de componente, cu toate sistemele de coordonate în condiții de egalitate.
Fără a insista pe o imagine picturală, un tensor este definit ca o entitate obiectivă care are componente care se schimbă în conformitate cu o lege de transformare, care este o generalizare a legii de transformare vectorială, dar care păstrează cele două proprietăți cheie ale acestei legi. Pentru comoditate, coordonatele sunt de obicei numerotate de la 1 la n, iar fiecare componentă a unui tensor este notată printr-o literă care are superscripturi și abonamente, fiecare preluând în mod independent valorile de la 1 la n. Astfel, un tensor reprezentat de componentele T ab c ar avea n 3 componente ca valorile a, b și c să curgă de la 1 la n. Scalarsele și vectorii constituie cazuri speciale de tensori, primii posedând o singură componentă pe fiecare sistem de coordonate, iar al doilea posedând n. Orice relație liniară între componentele tensiunii, cum ar fi 7R a bcd + 2S a bcd - 3T a bcd = 0, dacă este valabilă într-un singur sistem de coordonate, este valabilă în toate și reprezintă astfel o relație obiectivă și independentă de sistemele de coordonate, în ciuda lipsa unei reprezentări picturale.
Doi tensori, numiți tensor metric și tensor de curbură, prezintă un interes deosebit. Tensorul metric este folosit, de exemplu, la convertirea componentelor vectoriale în mărimi ale vectorilor. Pentru simplitate, luați în considerare cazul bidimensional cu coordonate perpendiculare simple. Lăsați vectorul V au componentele V 1, V 2. Apoi prin teorema pitagoreică aplicată triunghiului drept OAP pătratul mărimii lui V este dat de OP 2 = (V 1) 2 + (V 2) 2.

Ascunsă în această ecuație este tensorul metric. Este ascuns pentru că aici este format din 0 și 1 care nu sunt scrise. Dacă ecuația este rescrisă în formaOPOP 2 = 1 (V 1) 2 + 0V 1 V 2 + 0V 2 V 1 + 1 (V 2) 2, setul complet de componente (1, 0, 0, 1) al tensorului metric este aparent. Dacă se utilizează coordonate oblice, formula pentru OP 2 ia forma mai generalăOP 2 = g 11 (V 1) 2 + g 12 V 1 V 2 + g 21 V 2 V 1 + g 22 (V 2) 2, cantitățile g 11, g 12, g 21, g 22 fiind noile componente ale tensorului metric.
În afara tensorului metric este posibil să se construiască un tensor complicat, numit tensor de curbură, care reprezintă diferitele aspecte ale curburii intrinseci a spațiului n-dimensional din care face parte.
Tensorii au multe aplicații în geometrie și fizică. În crearea teoriei sale generale despre relativitate, Albert Einstein a susținut că legile fizicii trebuie să fie aceeași indiferent de sistemul de coordonate utilizat. Acest lucru l-a determinat să exprime acele legi în termeni de ecuații de tensiune. Din teoria sa specială a relativității se știa deja că timpul și spațiul sunt atât de strâns interrelaționate încât să constituie un spațiu-timp tridimensional indivizibil. Einstein a postulat că gravitația ar trebui să fie reprezentată doar în termenii tensiunii metrice a spațiului-timp în patru dimensiuni. Pentru a exprima legea relativistă a gravitației, el avea ca blocuri de construire tensorul metric și tensorul de curbură format din ea. Odată ce a decis să se limiteze la aceste blocuri de construcție, tocmai paucitatea lor l-a dus la o ecuație de tensiune esențial unică pentru legea gravitației, în care gravitația a apărut nu ca o forță, ci ca o manifestare a curburii spațiului-timp.
În timp ce tensiunile au fost studiate mai devreme, succesul teoriei generale a relativității lui Einstein a dat naștere interesului larg răspândit al matematicienilor și fizicienilor pentru tensori și aplicațiile lor.