Permutări și combinații, diferitele moduri în care obiectele dintr-un set pot fi selectate, în general fără înlocuire, pentru a forma subseturi. Această selecție de subseturi se numește permutare atunci când ordinea de selecție este un factor, o combinație atunci când ordinea nu este un factor. Luând în considerare raportul dintre numărul de subseturi dorite și numărul tuturor subseturilor posibile pentru multe jocuri de noroc din secolul al XVII-lea, matematicienii francezi Blaise Pascal și Pierre de Fermat au dat un impuls dezvoltării teoriei combinatoriei și probabilității.
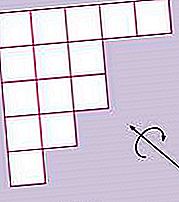
combinatorică: coeficienți binomiali
n obiecte se numește permutarea a n lucruri luate r la un moment dat. Numărul de permutări este
Conceptele și diferențele dintre permutații și combinații pot fi ilustrate prin examinarea tuturor diferitelor moduri în care o pereche de obiecte poate fi selectată dintre cinci obiecte distincte - cum ar fi literele A, B, C, D și E. Dacă ambele literele selectate și ordinea de selecție sunt luate în considerare, atunci următoarele 20 de rezultate sunt posibile:

Fiecare dintre aceste 20 de selecții posibile diferite se numește permutare. În special, ele sunt numite permutările a cinci obiecte luate două simultan, iar numărul de astfel de permutări posibile este notat cu simbolul 5 P 2, citit „5 permute 2.” În general, dacă există n obiecte disponibile pentru a selecta, iar permutațiile (P) trebuie formate folosind k de obiecte simultan, numărul de permutații diferite este notat prin simbolul n P k. O formulă pentru evaluarea sa este n P k = n! / (N - k)! Expresia n! - citită „n factorial” - indică faptul că toate numerele întregi pozitive consecutive de la 1 până la inclusiv n trebuie să fie înmulțite împreună, si 0! este definit ca fiind egal 1. De exemplu, folosind această formulă, numărul de permutări a cinci obiecte luate două simultan este

(Pentru k = n, n P k = n! Astfel, pentru 5 obiecte există 5! = 120 aranjamente.)
Pentru combinații, k obiecte sunt selectate dintr-un set de n obiecte pentru a produce subseturi fără a comanda. Contrastând exemplul de permutare anterioară cu combinația corespunzătoare, subseturile AB și BA nu mai sunt selecții distincte; eliminând astfel de cazuri, rămân doar 10 subseturi diferite - AB, AC, AD, AE, BC, BD, BE, CD, CE și DE.
Numărul acestor subseturi este notat cu n C k, citește „n alege k.“ Pentru combinații, deoarece k obiectele au k! aranjamente, există k! permutări nedistinguibile pentru fiecare alegere de k obiecte; de aici împărțind formula de permutare prin k! produce următoarea formulă de combinație:
Acesta este același cu coeficientul binomial (n, k) (vezi teorema binomială). De exemplu, numărul de combinații de cinci obiecte luate două simultan este
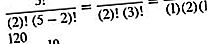
Formulele pentru n P k și n C k sunt numite formule de numărare, deoarece pot fi folosite pentru a număra numărul de permutări sau combinații posibile într-o situație dată, fără a fi obligat să le enumereze pe toate.

![Bătălia de la Mons. Primul Război Mondial [1914] Bătălia de la Mons. Primul Război Mondial [1914]](https://images.thetopknowledge.com/img/world-history/9/battle-mons-world-war-i-1914.jpg)










