Contribuții islamice
Contribuțiile islamice la matematică au început în jurul anului 825, când matematicianul Bagdad Muḥammad ibn Mūsā al-Khwārizmī a scris celebrul său tratat al-Kitāb al-mukhtaṣar fī ḥisāb al-jabr wa'l-muqābala (tradus în latină în secolul al XII-lea sub numele de Algebra et Almucabal, din care derivă termenul modern de algebră). Până la sfârșitul secolului al IX-lea, un corpus matematic important grecesc, incluzând lucrări ale lui Euclid, Arhimede (c. 285-212 / 211 a. Chr.), Apollonius din Perga (c. 262–190 a. Chr.), Ptolemeu (fl. Ad 127-145), și Diophantus, fuseseră traduse în arabă. În mod similar, matematica antică babiloniană și indiană, precum și contribuțiile mai recente ale înțelepților evrei, au fost puse la dispoziția savanților islamici. Acest fundal unic a permis crearea unui tip de matematică cu totul nou, care a fost mult mai mult decât o simplă amalgamare a acestor tradiții anterioare. Un studiu sistematic al metodelor de rezolvare a ecuațiilor cvadratice a constituit o preocupare centrală a matematicienilor islamici. O contribuție nu mai puțin centrală a fost legată de recepția și transmiterea de idei legate de sistemul indian de numerație, la care s-au adăugat fracții zecimale (fracții, cum ar fi 0.125, sau1 / 8).
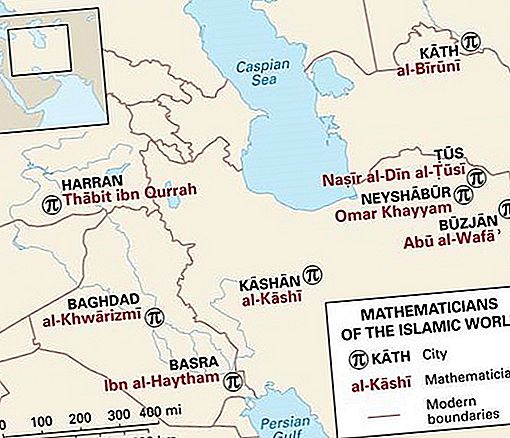
Opera algebrică a lui Al-Khwārizmī a întruchipat o mare parte din ceea ce a fost central pentru contribuțiile islamice. El a declarat că cartea sa intenționează să fie de valoare „practică”, cu toate că această definiție se aplică cu greu conținutului său. În prima parte a cărții sale, al-Khwārizmī a prezentat procedurile pentru soluționarea a șase tipuri de ecuații: pătrate rădăcini egale, pătrate numere egale, rădăcini numere egale, pătrate și rădăcini numere egale, pătrate și numere rădăcini egale și rădăcini și numere egale pătrate. În notație modernă, aceste ecuații ar fi declarate ax 2 = bx, ax 2 = c, bx = c, ax 2 + bx = c, ax 2 + c = bx și, respectiv, bx + c = ax 2. Numai numere pozitive au fost considerate coeficienți sau soluții legitime pentru ecuații. Mai mult, nici o reprezentare simbolică și nici o manipulare abstractă a simbolurilor nu au apărut în aceste probleme - chiar și cantitățile au fost scrise în cuvinte și nu în simboluri. De fapt, toate procedurile au fost descrise verbal. Acest lucru este ilustrat frumos de următoarea problemă tipică (recunoscută ca metoda modernă de completare a pătratului):
Care trebuie să fie pătratul care, atunci când este mărit cu 10 din propriile rădăcini, este de 39? Soluția este următoarea: Reduceți la jumătate numărul de rădăcini, care în cazul de față produce 5. Acest lucru îl multiplicați singur; produsul este 25. Adăugați acest lucru la 39; suma este 64. Acum luați rădăcina acestui, care este 8, și scade din ea jumătate din numărul rădăcinilor, care este 5; restul este 3. Aceasta este rădăcina pătratului pe care l-ați căutat.
În a doua parte a cărții sale, al-Khwārizmī a folosit propuneri preluate din Cartea a II-a a Elementelor lui Euclid pentru a oferi justificări geometrice pentru procedurile sale. După cum s-a menționat mai sus, în contextul lor original, acestea erau propuneri pur geometrice. Totuși, Al-Khwārizmī i-a conectat direct pentru prima dată la soluția ecuațiilor cvadratice. Metoda sa a reprezentat un semn distinctiv al demersului islamic de soluționare a ecuațiilor - sistematizează toate cazurile și apoi oferă o justificare geometrică, bazată pe surse grecești. Tipic acestei abordări a fost matematicianul și poetul persan Omar Khayyam Risālah fiʾl-barāhīn ʿalā masāʾil al-jabr waʾl-muqābalah (c. 1070; „Tratat de demonstrare a problemelor algebrei”), în care cunoștințele grecești cu privire la secțiuni conice (elipsi, parabolele și hiperbolele) a fost aplicată la întrebările care implică ecuații cubice.
Utilizarea argumentelor geometrice în stil grecesc în acest context a dus, de asemenea, la o slăbire treptată a anumitor constrângeri tradiționale grecești. În special, matematica islamică a permis și, într-adevăr, încurajată, combinația nerestricționată de mărimi comensurabile și incomensurabile în cadrul aceluiași cadru, precum și manipularea simultană a mărimilor de dimensiuni diferite ca parte a soluției unei probleme. De exemplu, matematicianul egiptean Abu Kāmil (c. 850–930) a tratat soluția unei ecuații cvadratice ca număr mai degrabă decât ca un segment de linie sau o zonă. Combinată cu sistemul zecimal, această abordare a fost fundamentală în dezvoltarea unei concepții mai abstracte și generale a numărului, ceea ce a fost esențial pentru crearea eventuală a unei idei abstracte a unei ecuații.