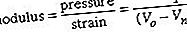Istoric de analiză
Grecii întâlnesc mărimi continue
Analiza constă în acele părți ale matematicii în care schimbarea continuă este importantă. Acestea includ studiul mișcării și geometria curbelor și a suprafețelor netede - în special, calculul tangențelor, zonelor și volumelor. Matematicii greci antici au făcut progrese mari atât în teoria, cât și în practica analizei. Teoria a fost forțată asupra lor aproximativ 500 de cca prin descoperirea pitagoreică a mărimilor iraționale și aproximativ 450 de cca prin paradoxurile mișcării lui Zeno.
Pitagoreii și numerele iraționale
Inițial, pitagoreii credeau că toate lucrurile pot fi măsurate prin numerele naturale discrete (1, 2, 3,
) și raporturile lor (fracții obișnuite sau numerele raționale). Această credință a fost însă zguduită de descoperirea că diagonala unui pătrat unitar (adică un pătrat ale cărui laturi au o lungime de 1) nu poate fi exprimată ca un număr rațional. Această descoperire a fost adusă de propria lor teoremă pitagoreică, care a stabilit că pătratul de pe ipotenuză a unui triunghi drept este egal cu suma pătratelor de pe celelalte două laturi - în nota modernă, c 2 = a 2 + b 2. Într-un pătrat unitar, diagonala este ipotenuză a unui triunghi dreptunghi, cu laturile a = b = 1; prin urmare, măsura sa este rădăcina pătrată de Ö2 - un număr irațional. Spre propriile lor intenții, pitagoreii arătaseră astfel că numerele raționale nu erau suficiente pentru măsurarea chiar și a unor simple obiecte geometrice. (Vezi Bara laterală: Incommensurabile.) Reacția lor a fost de a crea o aritmetică a segmentelor de linie, așa cum se găsește în Cartea a II-a a Elementelor lui Euclid (c. 300 bce), care includea o interpretare geometrică a numerelor raționale. Pentru greci, segmentele de linie erau mai generale decât numerele, deoarece includeau mărimi continue, dar și discrete.

Într-adevăr, rădăcina pătrată a √2 poate fi legată de numerele raționale doar printr-un proces infinit. Acest lucru a fost realizat de Euclid, care a studiat aritmetica atât a numerelor raționale, cât și a segmentelor de linie. Celebrul său algoritm euclidian, atunci când este aplicat la o pereche de numere naturale, conduce într-un număr finit de pași către cel mai mare divizor comun. Cu toate acestea, atunci când este aplicat pe o pereche de segmente de linie cu un raport irațional, cum ar fi rădăcina pătrată de Ö2 și 1, nu reușește să se termine. Euclid a folosit chiar această proprietate de nonterminare ca un criteriu pentru iraționalitate. Astfel, iraționalitatea a contestat conceptul grecesc de număr, forțându-i să se ocupe de procese infinite.
Paradoxurile lui Zeno și conceptul de mișcare
Așa cum rădăcina pătrată a √2 a fost o provocare pentru conceptul de număr al grecilor, paradoxurile lui Zeno au fost o provocare pentru conceptul lor de mișcare. În fizica sa (c. 350 a. Chr.), Aristotel l-a citat pe Zeno spunând:
Nu există nicio mișcare pentru că cea care este mișcată trebuie să ajungă la mijlocul [cursului] înainte de a ajunge la sfârșit.
Argumentele lui Zeno sunt cunoscute doar prin Aristotel, care le-a citat în principal pentru a le respinge. Probabil, Zeno a însemnat că, pentru a ajunge oriunde, trebuie să mergeți mai întâi la jumătatea drumului și înainte de acea pătrime a drumului și înainte de acea optime din drum și așa mai departe. Deoarece acest proces de reducere a distanțelor la jumătate ar continua la infinit (concept pe care grecii nu l-ar accepta posibil), Zeno a afirmat că „dovedește” că realitatea constă într-o ființă fără schimbări. Cu toate acestea, în ciuda dezlănțuirii lor de infinit, grecii au descoperit că conceptul era indispensabil în matematica mărimilor continue. Așa că au motivat infinitul cât se poate de fin, într-un cadru logic numit teoria proporțiilor și folosind metoda de epuizare.
Teoria proporțiilor a fost creată de Eudoxus în jur de 350 bce și păstrată în Cartea V a Elementelor lui Euclid. A stabilit o relație exactă între mărimile raționale și mărimile arbitrare, prin definirea a două mărimi care să fie egale dacă mărimile raționale mai mici decât ele ar fi aceleași. Cu alte cuvinte, două mărimi erau diferite numai dacă există o magnitudine rațională strict între ele. Această definiție a servit matematicienilor timp de două milenii și a deschis calea pentru aritmetizarea analizei în secolul al XIX-lea, în care numerele arbitrare au fost definite riguros în termeni de numere raționale. Teoria proporțiilor a fost primul tratament riguros al conceptului de limite, idee care se află în centrul analizei moderne. În termeni moderni, teoria lui Eudoxus a definit mărimile arbitrare ca limite ale mărimilor raționale, iar teoremele de bază despre suma, diferența și produsul mărimilor erau echivalente cu teoreme despre sumă, diferență și produsul limitelor.